11319. Maximize it!
Given two integers n and m,
find a real number a such that the value of f(1/2 + a) is maximized. It is known that
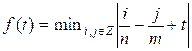
It can be proven that the maximum value of
the function f(t) is rational. Print this value in the form of an
irreducible fraction.
Input. Contains no more than 104
test cases. Each test case consists of a single line
containing two integers n and m (1 ≤ n, m ≤
109).
Output. For each test case, print the maximum value of f(1/2 + a) in the form of an irreducible
fraction p / q, where q > 0.
|
Sample
input |
Sample
output |
|
1 1 1 2 |
1/2 ¼ |
SOLUTION
mathematics
Algorithm analysis
Let’s consider the values that the
expression f(i, j) = i / n – j / m takes, where i,
j ∈ Z for fixed n and m. For example, f(n, m) = n / n – m
/ m = 0.
Let’s consider, for instance, the function f(i, j) = i / 3 – j / 5. Then
f(i, j) = ![]()
According
to the extended Euclidean algorithm, there always exist integers i and j, such that i / 3 – j / 5 = 1. Therefore, the smallest
positive value that the expression i / 3 – j / 5 can take is 1 / 15. From
this, it follows that this expression can take all possible values of the form k / 15, where k ∈ Z.
Theorem. If f(i,
j) = i / n – j / m, then this function takes values of the form k / LCM (n,
m), where k ∈ Z.
Proof. Indeed,
f(i, j) = i / n – j / m = ![]() =
=  =
=
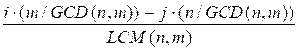
Since
the numbers m
/ GCD (n, m) and n / GCD(n,
m) are coprime, there always exists integers i and j such that the numerator of the
fraction equals 1. Therefore,
the function f(i, j) can take all possible values of the form k / LCM(n,
m), where k ∈ Z.
Now
let’s consider the original function
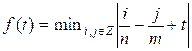
Its
values are the distances from the point t to the nearest point of the
form k / LCM(n,
m), where k ∈ Z. To maximize the function f(t),
the value of t should be chosen so that it is
exactly in the middle between the neighboring points k / LCM(n, m) and (k + 1) / LCM(n,
m), where k is an integer. The
value of the function at such a point is 1 / 2 * LCM(n, m), which will be the answer.
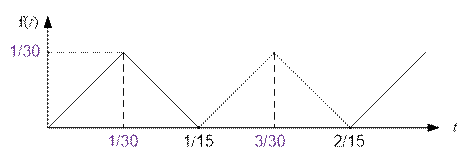
Example
Let  . It is
obvious that f(0) = 0. The equality f(1 / 15) = 0 holds because there exist integers i and j such
that i / 3 – j / 5 = -1 / 15 (for example, i = 1, j = 2). From this, it also follows that f(k / 15)
= 0, where k ∈ Z.
. It is
obvious that f(0) = 0. The equality f(1 / 15) = 0 holds because there exist integers i and j such
that i / 3 – j / 5 = -1 / 15 (for example, i = 1, j = 2). From this, it also follows that f(k / 15)
= 0, where k ∈ Z.
However, f(k / 15 + 1 / 30) = 1 / 30, and this will be
the maximum value of the function, as the point k / 15 + 1 / 30 is
at the maximum distance from the zeros of the function.
Algorithm implementation
The
gcd function computes the greatest common divisor of the numbers a and b.
long long gcd(long long a, long long b)
{
return b == 0 ? a : gcd(b, a % b);
}
The
lcm function computes the least common multiple of the numbers a and b.
long long lcm(long long a, long long b)
{
return a / gcd(a, b) * b;
}
The
main part of the program. Read the input data.
while (scanf("%lld %lld", &n, &m) == 2)
{
Compute
and print the result.
d = 2 * lcm(n, m);
printf("%lld/%lld\n", 1, d);
}